因果推断漫谈（二）：倾向性得分匹配介绍

Posted on In ,

倾向评分匹配是一种统计学方法，用于处理观察研究的数据。
在观察研究中，由于种种原因，数据偏差和混杂变量较多。
倾向评分匹配的方法正是为了减少这些偏差和混杂变量的影响，以便对实验组和对照组进行更合理的比较。

在上一篇文章 《因果推断漫谈（一）：掀开“因果推断”的面纱》 中，我们已经介绍了潜在结果模型、潜在结果模型中因果效应的定义，以及因果效应的可识别性。
这一篇文章来简单介绍一下 “倾向性得分匹配”（Propensity Score Matching），一个处理观察性研究（observational study）的经典方法。

因果推断数据集

在介绍倾向性得分匹配之前，我们介绍一个观察性研究中非常经典的数据集：The NSW Dataset。
这份数据最早是 Robert Lalonde 在论文 [1] 中使用的，所以这个数据集有的时候也被直接成为 “Lalonde”。
这份数据根据样本属性的齐全程度有几个不同的版本。
完整的情况可以参考 NSW Data。

随机实验数据 NSW Data Files (Dehejia-Wahha Sample) 是原始的 Lalonde’s NSW experimental data 中，样本 1974 年收入已知的一部分。

  1. 实验组：nswre74_treated.txt (185 observations)
  2. 对照组：nswre74_control.txt (260 observations)

“观察性研究” 数据的构造方式是取随机实验中的实验组，再搭配上一个通过其他渠道获得的对照组。
在 R 的非常好用的倾向性得分匹配 MatchIt 包里附带的数据是以下这个版本：

  1. 实验组：nswre74_treated.txt (185 observations)
  2. 对照组：cps3_controls.txt (429 observations)

在下文中，我们把随机实验数据称为 NSW-Data-Exp，把观察性研究数据称为 NSW-Data-Obs。

我们先看看数据集里具体都有些什么。

  • 干预 $T$: treat （是否接受了就业培训）
  • 样本属性 $X$: age, educ, black, hispan, married, nodegree (没有学位), re74
    (1974年的收入), re75 (1975年的收入)
  • 观察结果 $Y$: re78 (1978年的收入)

下表是每一个数据集按照 treat 分组后的统计结果。

  • 随机实验数据 NSW-Data-Exp 中：实验组和对照组样本的各类属性都是很接近的，实验组78年的收入比对照组高1794美元，可以认为是就业培训带来的因果效应。
  • 观察性研究数据 NSW-Data-Obs 中： 实验后，实验组用户的收入比对照组低635美金，容易造成“就业培训导致收入下降”的幻觉，但是仔细一看，实验组用户在实验前的收入也比对照组低很多，所以两组用户实验后的收入本来就没有什么可比性。
NSW-Data-Exp NSW-Data-Exp NSW-Data-Obs NSW-Data-Obs
treat 0 1 0 1
no. obs 260 185 429 185
age 25.05(0.44) 25.82(0.53) 28.03(0.52) 25.82(0.53)
educ 10.09(0.1) 10.35(0.15) 10.24(0.14) 10.35(0.15)
black 0.83(0.02) 0.84(0.03) 0.2(0.02) 0.84(0.03)
hispan 0.11(0.02) 0.06(0.02) 0.14(0.02) 0.06(0.02)
married 0.15(0.02) 0.19(0.03) 0.51(0.02) 0.19(0.03)
nodegree 0.83(0.02) 0.71(0.03) 0.6(0.02) 0.71(0.03)
re74 2107.03(352.75) 2095.57(359.27) 5619.24(327.76) 2095.57(359.27)
re75 1266.91(192.44) 1532.06(236.68) 2466.48(158.94) 1532.06(236.68)
re78 4554.8(340.09) 6349.14(578.42) 6984.17(352.17) 6349.14(578.42)

在互联网公司里做数据分析时，日常数据分析工作里也常常遇到类似的问题：
当我们想要分析一个产品特性、一个推荐策略、一个广告投放效果好不好时，我们的第一个尝试往往是把用户根据有没有命中或者有没有曝光 分成“有”和“没有”两组。
而在大部分时候，这两组用户是超级不同质的（例如被投放广告的用户可能是精挑细选的高潜力目标用户），所以比较起来也没有多大意义。

倾向性得分匹配

不论在 NSW-Data-Obs 这个数据集里，还是在上面提到的数据分析工作遇到的问题里，我们遇到的问题本质上都是想要比较的两个人群不同质。
如果我们想要消除两个人群之间的不同质，让两个人群之间可以比较，我们可以怎么做呢？

一个粗暴的思路是将实验组和对照组的样本做一下“匹配”。
例如，对于实验组的每一个样本，我们都去对照组里找一个一模一样的样本。
当样本属性全部都是离散的，并且属性的维度（个数）很小的时候，这么做也许是可以的。
当样本属性里有一些连续变量或者当样本属性的维度很高时，这么做太粗暴了，大部分人是找不到匹配对象的。

“倾向性得分匹配”，简单而言，是一种更加靠谱的找对象方案。
在介绍“倾向性得分匹配”的过程中，我们也同步用经典的 NSW-Data-obs 做一份数据分析。
做分析时，使用 R 的 MatchIt 包 [6]，完整的 Rmarkdown 见
yishilin14/causal_playground。

对于互联网公司的我，“样本”和“样本属性”这些名词有一些距离感，下文里用“用户”和“特征”代替，加强一下代入感。

倾向性得分的定义

“倾向性得分”的定义很直观，是一个用户属于实验组的“倾向性”： $e(x)=Pr[T=1|X=x]$。
倾向性得分是一种 “balancing score”。
所有的 balancing score 都有两个很好的性质，可以总结为以下两个定理。
如果感兴趣证明，可以参考 Imbens & Rubin 的 Causal Inference 教科书[4]第十二章。

Theorem 1 (Balancing Property). $ T_i ⊥ X_i | e(X_i)$。

Theorem 2 (Unconfoundedness). $ T_i ⊥ Y_{i0} , Y_{i1} | e(X_i)$。

直观来说，对于倾向性得分相同的一群用户，treatment和特征是独立的，treatment和潜在结果也是独立的。
因此，理论上，如果我们对每一个实验组用户都在对照组里匹配一个得分相等（要求有点严苛）的用户，我们就能得到同质的实验组和对照组，就可以假装我们做了一个A/B Test了，接着就可以随意地进行组间比较了。

上面这段话具体实施起来，可以分为以下几个步骤。

  1. 倾向性得分估算：倾向性得分一般来说是未知的，怎么估算？
  2. 倾向性得分匹配：怎么匹配？
  3. 平衡性检查：怎么量化匹配效果？
  4. 因果效应估算：怎么从匹配后的两组用户中得到因果效应？
  5. 敏感度分析：分析结论对于混淆变量选没选对（不满足 unconfoundedness ）是不是很敏感？

接下来，我们一个一个来看。

Step 1: 倾向性得分估算

这一步说白了，就是一个建模问题。
一般来说，按需做一下特征预处理，然后套一下 LR 就可以了。
如果发现某些变量匹配效果不好（之后会介绍如何量化“匹配效果”），可以考虑加入一些高阶项，从这一步重来一遍。

个人也试过使用 LR + LightGBM 估算倾向性得分，然后选 AUC 比较高的模型，在自己生成的仿真数据上看了一下，确实效果好一些。
但是关于倾向性得分估算到底要不要上复杂模型，其实是一个
trade-off，如果每次做分析都要做参数网格搜索甚至需要人肉调参，好像也不太实际对吧。

Step 2: 倾向性得分匹配

假设我们已经有了每个用户的倾向性得分，我们的目标是针对目前的实验组用户，匹配得到一个近乎于同质的对照组。

当用户量足够时候，一个简单做法是进行一对一无放回匹配：对于每一个实验组用户，我们去对照组里找一个倾向性得分最近的用户，把他们配成一对。匹配过程中，可以限制一下配对用户的得分差异不能超过某一个阈值，配不上就算了，以防把“太不相似”的用户匹配在一起。

在实现匹配时，有很多细节有很多选项，下面列一下个人认为比较常见的。
和机器学习里调每个参数都对应着某些 trade-off 类似，这里每个选项背后也都有对应的 bias-variance 的 trade-off 的，就不细说。

  1. 匹配用的得分：可选原始倾向性得分 $e(x)$ 或者得分的 logit
    $l(x)=ln(e(x)/(1-e(x)))$，接下来都统一用 $e$ 表示。
  2. 修剪（trimming）：秉承着“希望下一个通用的结论”的思路，可以先筛选掉倾向性得分比较“极端”的用户，例如在现实中不大可能出现在实验组里的对照组用户。常见的做法是保留得分在 $[ e_{min}, e_{max} ]$ 这个区间的用户，关于区间选择，下面是两个例子。
    • 实验组和对照组用户得分区间的交集
    • 只保留区间中部 90% 或者 95%，如取原始得分在 $[0.05, 0.95]$ 的用户
  3. 匹配（matching)：实验组对对照组根据得分进行匹配时候，比较常见的有以下两种方法。
    • nearest neighbors: 进行1对K有放回或无放回匹配
    • radius: 对每个实验组用户，匹配上所有得分差异小于指定 radius 的用户
  4. 得分差异上限（caliper）：当我们匹配用户的时候，我们要求每一对用户的得分差异不超过指定
    的 caliper，“强扭的瓜不甜”，匹配不好就不要放弃吧。

接下通过短短几行的代码，配平一下经典数据集 NSW-Data-Obs。
MatchIt 会帮我们估算好倾向性得分，再进行匹配。
参数的名字都很直观，就不唠叨。
至于参数是怎么选的，这是我配来配去，发现“配平效果”最好的一组参数。

1
2
3
4
5
6
7
8
set.seed(42)
m.out <- matchit(data = nsw_data_obs,
                 formula = treat ~ age + I(age^2) + I(age^3) + educ + black + hispan + married + 
                                I(re74/1000) + I(re75/1000),
                 method = "nearest",
                 distance = "logit",
                 replace = FALSE,
                 caliper = 0.05)

Step 3: 平衡性检查

怎么衡量“配平效果“呢？

比较直观的是看倾向性得分在匹配前后的分布、以及特征在匹配前后的QQ-Plot。
MatchIt 自带了这些，两行代码搞定。

下面两张图里是 NSW-Data-Obs 的配平结果。
可以看出，匹配后的实验组和对照组的倾向性得分分布更加接近，变量分布也更接近。
其实匹配后的“倾向性得分”分布并不是非常完美，这个数据里的样本实在是太少了。

1
2
plot(m.out, type = "hist", interactive = F)
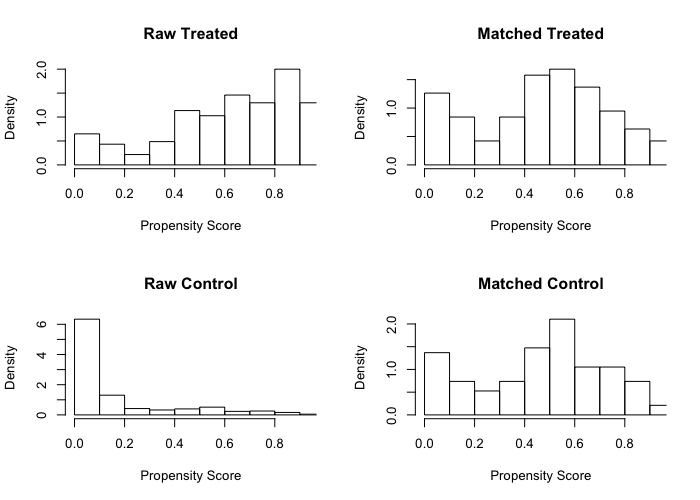
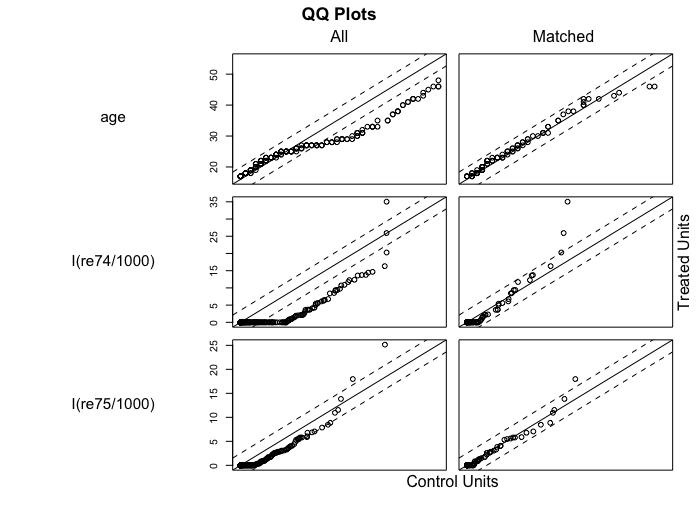
plot(m.out, type = "QQ", interactive = F, which.xs = c("age", "I(re74/1000)", "I(re75/1000)"))

看图毕竟还是不够直观，我们还需要配平效果的量化指标。
Coursera 上的公开课 “A Crash Course in Causality: Inferring Causal Effects from
Observational Data” 里介绍了量化指标 Standarized Mean Difference (SMD)。
SMD 的一种计算方式为：（实验组均值-对照组均值）/实验组标准差。
公开课里的教授说，一般如果一个变量的 SMD 不超过0.1，一般就可以认为这个变量的配平质量可以接受。
当一个变量的SMD超过0.1的时候，需要凭经验确认一下那个变量是不是没有那么重要。

MatchIt 里自带了一个函数，可以计算配平前后每个变量的各类统计结果，其中也包括了 SMD。
这里我们只看看配平后的效果。
配平后 SMD 绝对值的最大值是0.09，可以认为配平质量可以接受。

1
summary(m.out, standardize = T)$sum.matched
Means Treated Means Control SD Control Std. Mean Diff. eCDF Med eCDF Mean eCDF Max
distance 0.48 0.47 0.25 0.03 0.01 0.01 0.04
age 25.28 24.79 8.40 0.07 0.02 0.02 0.08
I(age^2) 702.42 684.28 518.77 0.04 0.02 0.02 0.08
I(age^3) 21480.53 21211.74 26553.46 0.01 0.02 0.02 0.08
educ 10.21 10.03 2.98 0.09 0.04 0.05 0.12
black 0.69 0.72 0.45 -0.06 0.01 0.01 0.02
hispan 0.12 0.11 0.31 0.04 0.01 0.01 0.01
married 0.26 0.25 0.44 0.03 0.01 0.01 0.01
I(re74/1000) 2.50 2.59 4.16 -0.02 0.05 0.10 0.33
I(re75/1000) 1.76 1.94 3.12 -0.05 0.02 0.04 0.16

Step 4: 因果效应推断

我们的目标是推断 ATT (Average Treatment Effect on the Treated)。
回顾一下，ATT 的定义为 $ATT=E[Y_1 - Y_0 | T=1]$。
现在我们已经有一对接近同质的实验组和对照组了，有很多方法可以用来估算 ATT 。
个人感觉两种比较直观是：

  1. 直接比较匹配后的实验组和对照组
  2. 拟合一个由干预和用户特征预测观察结果的线形模型，看看干预 $T$ 的系数是多少
  3. ……

对于NSW-Data-obs，以上两种方法估算的ATT结果都差不多，大致为1900到2000美金，和1794美金这个 ground truth 差不太多（毕竟不配平直接估算是-635美金啊）。

方法 ATT ATT 标准差 ATT 95%置信区间
直接比较 1986 1062 (-112, 4083)
拟合 $Y = T+X$ 1907 1075 (-215, 4029)

代码如下（MatchIt 已经完成了它的使命，这一部分就得自己写了）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
m.data <- match.data(m.out)

# Direct compare
res <- wtd.t.test(m.data$re78[m.data$treat == 1],
                  m.data$re78[m.data$treat == 0],
                  weight = m.data$weights[m.data$treat == 1],
                  weighty = m.data$weights[m.data$treat == 0])
print(res)
mu <- res$additional[1]
std <- res$additional[4]
cat("Confidence interval: ", sapply(qt(c(0.025, 0.975), coef(res)["df"]), function(x){return(mu+x*std)}), "\n")

# Fit
att.fml <- re78 ~ treat + age + educ + black + hispan + married + nodegree + re74 + re75
fit <- lm(att.fml, data = m.data, weights = m.data$weights)
summary(fit)
cat("Confidence interval: ", confint(fit, "treat", 0.95), "\n")

Step 5: 敏感性检查

敏感性分析的方法是独立于倾向性得分匹配的。
主要的目标是衡量当混淆变量（特征）不满足 unconfoundedness 时，分析结论是不是 robust。
一个简单的做法是去掉一个或者多个混淆变量重复上面的过程，如果分析结论翻脸如翻书，说明
unconfoundedness 要么依赖于所有特征，要么不成立。

其它更系统的敏感性检查方案，还在学习中，之后再写一篇。

倾向性得分匹配综述

关于倾向性得分匹配，有一篇引用超过4000的 Some practical guidance for the implementation of propensity score matching [5]，感兴趣的小伙伴可以读一读。上面所写，只是其中的一个小小子集。

倾向性得分的其它打开方式

倾向性得分除了用来匹配，还有其它的用法。
例如，我们可以用倾向性得分来对用户进行分组，称为 subclassification。
我们还可以用倾向性得分来对用户进行加权，称为 Inverse Propensity Score Weighting (IPSW)。
万变不离其中，目标都是为了消除两组用户的不同质导致的分析偏差。

小结

这一篇文章介绍了“倾向性得分匹配”这个方法。
这个方法的本质目标是消除观察性研究中实验组和对照组用户的不同质，进而得到因果效应的估算。

方法思路虽然简单，真正使用起来还是有点让人不知所措，光是匹配参数（trimming、匹配方法、caliper等等）就有好多不同的选择，还是需要多加练习。
刚刚入门，如果有哪位好心人有什么系统性地选择匹配方法的方法，还请多多指教。

参考资料

  1. LaLonde R J. Evaluating the econometric evaluations of training programs with experimental data[J]. The American economic review, 1986: 604-620.
  2. Dehejia R H, Wahba S. Causal effects in nonexperimental studies: Reevaluating the evaluation of training programs[J]. Journal of the American statistical Association, 1999, 94(448): 1053-1062.
  3. Dehejia R H, Wahba S. Propensity score-matching methods for nonexperimental causal studies[J]. Review of Economics and statistics, 2002, 84(1): 151-161.
  4. Imbens G W, Rubin D B. Causal inference in statistics, social, and biomedical sciences[M]. Cambridge University Press, 2015.
  5. Caliendo M, Kopeinig S. Some practical guidance for the implementation of propensity score matching[J]. Journal of economic surveys, 2008, 22(1): 31-72.
  6. MatchIt 文档：https://r.iq.harvard.edu/docs/matchit/2.4-20/matchit.pdf